SGU乱做
虽然比较晚了
但是听说SGU质量都比较好，所以开刷了。P.S.感觉SGU的乱搞题比较多啊，真是开心。
upd:en没错这东西已经坑掉了。。
101：maya第二题劳资就不会做，一开始想到了是要搞成若干个环加一条链，但是不知道怎么找无向图中的环。然后发现网上都使用了一个神奇的DFS，因为DFS未走过的边，从起点开始第一次无法继续递归只会是到另外一个奇度数点或者自己，所以递归时先递归所到达的点再记录边，这样记录的边回是连续的。然后判断有没有解就是连通性和点度数判断。具体看代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
#define N 2005
int c[N][2],fi[N],n,m=-1,li[N],ss=1,cnt=0,s[N];bool b[N];
inline int Read()
{
int x=0;char y;
do y=getchar(); while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return x;
}
inline void Line(int y,int x)
{
c[++ss][0]=y;c[ss][1]=fi[x];fi[x]=ss;s[x]++;
c[++ss][0]=x;c[ss][1]=fi[y];fi[y]=ss;s[y]++;
}
void DFF(int x)
{
b[x]=1;
for (int i=fi[x];i;i=c[i][1])
if (!b[c[i][0]]) DFF(c[i][0]);
return;
}
bool Check()
{
for (int i=0;i<=6;i++)
if (fi[i]&&!b[i]) {DFF(i);break;}
for (int i=0;i<=6;i++)
if (fi[i]&&!b[i]) return 1;
for (int i=0,j=0;i<=6;i++)
{
j+=s[i]&1;
if (s[i]&1) m=i;
if (m==-1&&s[i]) m=i;
if (j>2) return 1;
}
memset(b,0,sizeof(b));
return 0;
}
void DFS(int x)
{
for (int i=fi[x];i;i=c[i][1])
if (!b[i])
b[i]=b[i^1]=1,DFS(c[i][0]),li[++cnt]=i;
return;
}
int main()
{
n=Read();
for (int i=1;i<=n;i++) Line(Read(),Read());
if (Check()) puts("No solution");else
{
DFS(m);
for (int i=1;i<=cnt;i++)
printf("%d ",li[i] >> 1),
putchar(li[i]&1?'+':'-'),putchar('\n');
}
return 0;
}
108：本来以为O(n)会挂，都想要分块打表了，没想到筛是可以过的。话说内存卡的丧心病狂
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
#define N 5050
#define M 150
#define fr first
#define sc second
pair <int,int> b[N];
int n,m,s=0,v=0,cnt=0,c[N],d[N];bool a[M];
inline int Read()
{
int x=0;char y;
do y=getchar(); while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return x;
}
int main()
{
n=Read();m=Read();
for (int i=1;i<=m;i++) b[i].fr=Read(),b[i].sc=i;
sort(b+1,b+m+1);
for (int i=1;i<=n;i++)
{
int j=0,k=i,l=i%64;
while (k) j+=k%10,k/=10;
a[(j+i)%64]=1;
if (!a[l]) s++;
while (!a[l]&&s==b[v+1].fr) c[++v]=i;
a[l]=0;
}
cout <<s<<endl;
for (int i=1;i<=m;i++) d[b[i].sc]=c[i];
for (int i=1;i<m;i++)
printf("%d ",d[i]);
printf("%d\n",d[m]);
return 0;
}
SGU109：构造，乱搞。
SGU110：反正是一堆向量在乱搞，可以推出来。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
#define N 105
#define eps 1e-6
#define INF 0x7f7f7f7f
struct Point
{
double x,y,z;
} a[N],S,T;
double r[N];
int n,m;
Point operator+ (const Point &x,const Point &y)
{return (Point){x.x+y.x,x.y+y.y,x.z+y.z};}
Point operator- (const Point &x,const Point &y)
{return (Point){x.x-y.x,x.y-y.y,x.z-y.z};}
Point operator* (const Point &x,const double &y)
{return (Point){x.x*y,x.y*y,x.z*y};}
inline double min(double x,double y)
{return x<y?x:y;}
inline double sqr(double x)
{return x*x;}
inline double dis(Point x,Point y)
{return sqrt(sqr(x.x-y.x)+sqr(x.y-y.y)+sqr(x.z-y.z));}
inline int Read()
{
int x=0;char y;bool z=0;
do y=getchar(),z|=y=='-'; while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return z?-x:x;
}
Point Vertical(Point x,Point y,Point z)
{
double q=dis(x,y),w=dis(y,z),e;
e=(sqr(q)+sqr(w)-sqr(dis(x,z)))/(2*q*w);
return y+(z-y)*(q*e/w);
}
Point Intersect(Point x,Point y,Point z,double u)
{
double q=dis(x,y),w=dis(y,z),e=q-sqrt(sqr(u)-sqr(w));
return x+(y-x)*(e/q);
}
int main()
{
n=Read();
for (int i=1;i<=n;i++)
a[i].x=Read(),a[i].y=Read(),a[i].z=Read(),r[i]=Read();
scanf("%lf%lf%lf%lf%lf%lf",&S.x,&S.y,&S.z,&T.x,&T.y,&T.z);
for (int i=1;i<=11;i++)
{
Point s,t;double mi=INF;int q=0;
for (int j=1;j<=n;j++)
{
Point k=Vertical(a[j],S,T),l;
if (dis(k,a[j])>r[j]+eps||
abs(dis(T,k)-dis(S,T)-dis(k,S))<eps) continue;
l=Intersect(S,k,a[j],r[j]);
if (dis(l,S)>mi) continue;
mi=dis(l,S);s=l;t=S+(Vertical(S,l,a[j])-S)*2;q=j;
}
if (mi==INF) {printf("\n");break;}
if (i!=11) printf("%d ",q);else
puts("etc.");
S=s;T=t;
}
return 0;
}
SGU111：之前在codevs做过，让人感觉丧心病狂（很久以前写的太丑了还是不贴代码的好）
SGU118：打表发现f就是123456789的循环，然后直接做了，发现结论之后证明是很容易的。
SGU119：一眼感觉就是所有(A0*k)%N*X+(B0*k)%N*Y，证明都没证明直接交了= =
SGU120：恶心的计算几何。旋转二维向量有公式的（@baidu向量旋转矩阵），然而我之前的笔记都记得我看不清了，结果wa了n久= =
#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 150
#define eps 1e-10
const double pi=acos(-1.0);
struct Point
{double x,y;} a[N],S,T;
int n,m,s1,s2;double r,d,p;
Point operator+ (const Point &x,const Point &y)
{return (Point){x.x+y.x,x.y+y.y};}
Point operator- (const Point &x,const Point &y)
{return (Point){x.x-y.x,x.y-y.y};}
Point operator* (const Point &x,const double &y)
{return (Point){x.x*y,x.y*y};}
inline Point Rotate(Point x,double y)
{double i=cos(y),j=sin(y);return (Point){x.x*i-x.y*j,x.x*j+x.y*i};}
inline double sqr(double x)
{return x*x;}
inline double dis(Point x,Point y)
{return sqrt(sqr(x.x-y.x)+sqr(x.y-y.y));}
inline Point Zoom(Point x,double y)
{return x*(y/(sqrt(sqr(x.x)+sqr(x.y))));}
int main()
{
cin >>n>>s1>>s2;
scanf("%lf%lf%lf%lf",&a[s1].x,&a[s1].y,&a[s2].x,&a[s2].y);
r=2*pi*min(abs(s1-s2),n-abs(s1-s2))/n;p=(pi-r)/2;
r=dis(a[s1],a[s2])/sqrt(2*(1-cos(r)));
d=2*pi/n;r*=sqrt(2-2*cos(d));
if (s2!=s1%n+1)
{
if ((n+s2-s1)%n<=n/2)
p=(pi-d)/2-p,a[s1%n+1]=a[s1]+Zoom(Rotate(a[s2]-a[s1],p),r);else
p=p+(pi-d)/2,a[s1%n+1]=a[s1]+Zoom(Rotate(a[s2]-a[s1],p),r);
}
for (int i=(s1+1)%n+1;i!=s1;i=i%n+1)
{
Point k=a[(i+n-2)%n+1],l=a[(i+n-3)%n+1];
a[i]=k+Rotate(k-l,2*pi-d);
}
for (int i=1;i<=n;i++)
printf("%.6lf %.6lf\n",a[i].x+eps,a[i].y+eps);
return 0;
}
SGU121：感觉这道题真是莫名其妙啊，题解也都是造的出反例的乱搞，真是不知道什么鬼。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
#define N 105
int a[N][N],c[N][N],sz[N],n,m;bool b[N][2];
inline int Read()
{
int x=0;char y;
do y=getchar(); while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return x;
}
void DFS(int x,int y)
{
for (int i=1;i<=sz[x];i++)
{
int k=a[x][i];
if (!c[x][k])
c[x][k]=c[k][x]=y,b[x][2-y]=b[k][2-y]=1,DFS(k,y=3-y);
}
}
int main()
{
n=Read();
for (int i=1,k;i<=n;i++)
while (k=Read()) a[i][++sz[i]]=k;
for (int i=1;i<=n;i++)
if (sz[i]&1) DFS(i,1);
for (int i=1;i<=n;i++)
if (!(sz[i]&1)) DFS(i,1);
for (int i=1;i<=n;i++)
if ((!b[i][0]||!b[i][1])&&sz[i]>1) m=-1;
if (m) {puts("No solution");return 0;}
for (int i=1;i<=n;i++)
{
for (int j=1;j<=sz[i];j++)
printf("%d ",c[i][a[i][j]]);
puts("0");
}
return 0;
}
SGU122：组合数学原题，感觉也是比较诡异= =
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
#define N 1050
bool a[N][N],b[N];
int n,m,s[N],S,T,ne[N][2],ans=0,li[N];
inline int Read()
{
int x=0;char y;
do y=getchar(); while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return y=='\n'||y==EOF?-x:x;
}
void Ins(int x)
{
for (int i=1;i<=n;i++)
if (a[x][i]&&!b[i]) s[i]++;
ans++;b[x]=1;
}
int DFS(int x,bool y)
{
for (int i=1;i<=n;i++)
if (a[x][i]&&!b[i])
{Ins(i);ne[x][y]=i;ne[i][!y]=x;return DFS(i,y);}
return x;
}
void Reverse(int x,int y)
{
int cnt=0;
for (int i=ne[x][1];i;i=ne[i][1])
li[++cnt]=i;
for (int i=cnt;i>=1;i--)
ne[x][1]=li[i],ne[li[i]][0]=x,x=li[i];
ne[T=li[1]][1]=S;ne[S][0]=T;
}
int main()
{
n=Read();n=-n;
for (int i=1;i<=n;i++)
do
{
int k=Read();a[i][abs(k)]=1;
if (k<0) break;
} while (true);
Ins(S=T=b[1]=1);ne[1][1]=ne[1][0]=1;
while (ans!=n)
{
int t=0;
for (int i=1;i<=n;i++)
if (!b[i]&&s[i])
{
for (int j=1;j<=n;j++)
if (a[i][j]&&b[j])
{
S=i;ne[i][1]=j;T=ne[j][0];
ne[T][1]=0;ne[j][0]=i;Ins(i);break;
}
break;
}
S=DFS(S,0);T=DFS(T,1);
for (int i=S;i!=T;i=ne[i][1])
if (a[i][T]&&a[ne[i][1]][S])
{Reverse(i,T);break;}
}
cout <<1<<' ';
for (int i=ne[1][1];i!=1;i=ne[i][1])
printf("%d ",i);
cout <<1<<endl;
return 0;
}
SGU124：本来以为是凸多边形，然后就想用叉积什么的直接搞，然后果wa。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
#define N 20050
#define eps 1e-8
struct Point
{int x,y;} Edge[N][2],li[N],S;
Point operator- (const Point &x,const Point &y)
{return (Point){x.x-y.x,x.y-y.y};}
int n,m,ss=1,ln[N][2],s;
inline int Read()
{
int x=0;char y;bool z=0;
do y=getchar(),z|=y=='-'; while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return z?-x:x;
}
inline double sqr(double x)
{return x*x;}
inline double dis(Point x,Point y)
{return sqrt(sqr(x.x-y.x)+sqr(x.y-y.y));}
inline double Cha(Point x,Point y)
{return x.x*y.y-x.y*y.x;}
int main()
{
n=Read();
for (int i=1;i<=n;i++)
Edge[i][0].x=li[i*2-1].x=Read(),
Edge[i][0].y=li[i*2-1].y=Read(),
Edge[i][1].x=li[i*2].x=Read(),
Edge[i][1].y=li[i*2].y=Read();
S.x=Read();S.y=Read();
for (int i=1;i<=n;i++)
if (fabs(dis(Edge[i][0],Edge[i][1])-dis(Edge[i][0],S)-
dis(Edge[i][1],S))<=eps)
{puts("BORDER");return 0;}
for (int i=1;i<=n;i++)
{
if (Edge[i][0].y>Edge[i][1].y)
swap(Edge[i][0],Edge[i][1]);
if (Cha(Edge[i][0]-S,Edge[i][1]-S)<0&&
Edge[i][0].y<=S.y&&Edge[i][1].y>S.y)
s++;
}
if (s&1) puts("INSIDE");else puts("OUTSIDE");
return 0;
}
BZOJ1016最小生成树计数
本来是Matrix-Tree裸题，然后不知道怎么写挂了，然后再网上看到了一种奇怪的做法：
首先处理出一棵最小生成树，然后统计不同权值在树上的出现的次数，
有个性质是显然的：最小生成树上的不同权值的个数一定是上面那样子的（虽然不会证但是总感觉很有道理）
然后就按权值从小到大，处理出权值为v的所有边的不会使当前图有环的方案s，然后选择其中一种方案的边加入当前图中，最后把所有s乘起来。
至于证明：数学归纳法假设前i种权值选择好了之后的图联通情况都是相同的，然后加入k条边，如果有两种方案使得处理后联通情况不同那么两种方案的并一定会更优，所以是可以这么搞的。然后这么看所有权值的边选择独立，所以可以乘法原理乘起来。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
#define N 105
#define M 31011
struct Line
{
int x,y,v;
} a[N*10];
int n,m,ss=1,fa[N],s[N*10],cnt=0,h[N*10],ans=1;
bool b[N*10];
inline int Read()
{
int x=0;char y;
do y=getchar(); while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return x;
}
int Find(int x)
{return x==fa[x]?x:(fa[x]=Find(fa[x]));}
inline bool cmp(Line x,Line y)
{return x.v<y.v;}
int find(int x)
{return x==fa[x]?x:find(fa[x]);}
int DFS(int x,int y,int z)
{
int i=find(a[x].x),j=find(a[x].y),k=0;
if (x==z) return y==0;
if (i!=j&&y) {fa[i]=j;k=DFS(x+1,y-1,z);fa[i]=i;}
k+=DFS(x+1,y,z);
return k;
}
int main()
{
int i,j,k,l,q,w,e=0;
n=Read();m=Read();
for (i=1;i<=m;i++)
a[i].x=Read(),a[i].y=Read(),a[i].v=Read();
sort(a+1,a+m+1,cmp);
for (i=1;i<=n;i++) fa[i]=i;
for (i=1;i<=m;i++)
{
k=Find(a[i].x);l=Find(a[i].y);
if (k!=l)
fa[k]=l,e++,b[i]=1;
}
if (e!=n-1)
{printf("0\n");return 0;}
for (i=1;i<=m;i++)
{
if (a[i].v!=a[i-1].v) h[++cnt]=i;
s[cnt]+=b[i];
}
h[cnt+1]=m+1;
for (i=1;i<=n;i++) fa[i]=i;
for (i=1;i<=cnt;i++)
{
ans=(ans*DFS(h[i],s[i],h[i+1]))%M;
for (j=h[i];j<h[i+1];j++)
if (b[j])
q=find(a[j].x),w=find(a[j].y),fa[q]=w;
}
cout <<ans<<endl;
return 0;
}
NOI题乱做
RT，放些最近写的NOI老题。
BZOJ3668起床困难综合症
直接爆搞
#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 100050
#define INF 0x7f7f7f7f
#define ll long long
ll a[N][2],n,m,ans=0,ss,t=0;
inline ll aa(int x)
{
ll i,j,k,l,q,w,e=x;
for (i=1;i<=n;i++)
if (a[i][0]==1)
e=e&(a[i][1]&ss);else
e=a[i][0]==2?e^(a[i][1]&ss):e|(a[i][1]&ss);
return e;
}
int main()
{
ll i,j,k,l,q,w,e;
char b[20];
memset(a,0,sizeof(a));
scanf("%lld%lld",&n,&m);
for (i=1;i<=n;i++)
{
scanf("%s%lld",b,&a[i][1]);
if (b[0]=='A'&&b[1]=='N')
a[i][0]=1;else
a[i][0]=b[0]=='X'&&b[1]=='O'?2:3;
}
for (ss=1 << 29;ss;ss >>= 1)
{
i=aa(0);
j=t+ss>m?-1:aa(ss);
if (i>=j)
ans+=i;else
ans+=j,t+=ss;
}
cout <<ans<<endl;
return 0;
}
BZOJ3669魔法森林：LCT
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <cmath>
#include <algorithm>
using namespace std;
#define N 100050
#define INF 0x7f7f7f7f
struct Line
{
int s,v,a1,b1;
} a[N];
int c[N][2],t[N],fa[N],rf[N],ft[N],ma[N];
int n,m,ans=INF,ss;
bool fz[N];
inline int Read()
{
int x=0;char y;
do y=getchar(); while (y<'0'||y>'9');
do x=(x << 3)+(x << 1)+y-'0',y=getchar();
while (y>='0'&&y<='9');
return x;
}
inline bool cmp(Line x,Line y)
{
return x.a1<y.a1;
}
inline void Update(int x)
{
ma[x]=max(ma[c[x][0]],max(ma[c[x][1]],x>n?t[x]:-INF));
return;
}
inline void fzj(int x)
{
if (!x||!fz[x])
return;
fz[c[x][0]]=!fz[c[x][0]];fz[c[x][1]]=!fz[c[x][1]];
swap(c[x][0],c[x][1]);
fz[0]=fz[x]=0;
return;
}
inline void Rotate(int x)
{
int i=fa[x],j=fa[fa[x]],k=x==c[i][0];
if (j)
c[j][c[j][1]==i]=x;else
rf[x]=rf[i],rf[i]=0;
fa[c[x][k]]=c[x][k]?i:0;
c[i][1-k]=c[x][k];fa[i]=x;
c[x][k]=i;fa[x]=j;
Update(i);
return;
}
inline void DFS(int x)
{
if (fa[x])
DFS(fa[x]);
fzj(x);fzj(c[x][0]);fzj(c[x][1]);
return;
}
inline void Splay(int x)
{
DFS(x);
while (fa[x])
{
if (fa[fa[x]])
Rotate(c[fa[fa[x]]][0]==fa[x]^c[fa[x]][0]==x?x:fa[x]);
Rotate(x);
}
Update(x);
return;
}
inline void Access(int x)
{
int i=0;
while (x)
{
Splay(x);
rf[c[x][1]]=fa[i]=x;
fa[c[x][1]]=rf[i]=0;
c[x][1]=i;Update(x);
i=x;x=rf[x];
}
rf[0]=fa[0]=0;
return;
}
inline void Cg_rt(int x)
{
Access(x);Splay(x);
fz[x]=1;fzj(x);
return;
}
inline void Line(int x,int y)
{
Cg_rt(x);rf[x]=y;
return;
}
inline void Delete(int x)
{
Splay(x);fa[c[x][0]]=fa[c[x][1]]=0;
c[x][0]=c[x][1]=0;
return;
}
inline int Lma(int x)
{
if (ma[x]==t[x])
return x;else
return ma[c[x][0]]==ma[x]?Lma(c[x][0]):Lma(c[x][1]);
}
inline int Find(int x)
{
if (x==ft[x])
return x;
ft[x]=Find(ft[x]);
return ft[x];
}
int main()
{
int i,j,k,l,q,w,e;
memset(t,0,sizeof(t));memset(c,0,sizeof(c));
memset(fa,0,sizeof(fa));memset(rf,0,sizeof(rf));
memset(ft,0,sizeof(ft));memset(ma,0,sizeof(ma));
memset(fz,0,sizeof(fz));
scanf("%d%d",&n,&m);
ma[0]=-INF;
for (i=1;i<=n;i++)
ft[i]=i;
ss=n;
for (i=1;i<=m;i++)
scanf("%d%d%d%d",&a[i].s,&a[i].v,&a[i].a1,&a[i].b1);
sort(a+1,a+m+1,cmp);
for (i=1;i<=m;i++)
if (a[i].s!=a[i].v)
{
k=Find(a[i].s);l=Find(a[i].v);
if (k!=l)
{
ft[k]=l;t[++ss]=ma[ss]=a[i].b1;
Line(a[i].s,ss);Line(a[i].v,ss);
}else
{
Cg_rt(a[i].s);Access(a[i].v);Splay(a[i].v);
k=Lma(a[i].v);
if (t[k]>a[i].b1)
{
Delete(k);ma[k]=t[k]=a[i].b1;
Line(a[i].s,k);Line(a[i].v,k);
}
}
if (Find(1)==Find(n))
{
Cg_rt(1);Access(n);Splay(n);
ans=min(ans,a[i].a1+t[Lma(n)]);
}
}
ans=ans==INF?-1:ans;
cout <<ans<<endl;
return 0;
}
BZOJ3670动物园：建一棵Fail树（貌似也有的叫KMP自动机？），然后我写了个倍增，但是怎么调都只有60分（明明在本机上用同一组数据是答案正确的但是uoj上怎么都会错是smg？）。感觉最近都是的，未免对这种复杂度太有自信了吧= =，结果好几次都没去想正解就直接贴这种挂的代码。然后想线性的做法，en，没想出来，orzei了hzwer的（wulala说这个还算不难想吧，我思维弱已经成了常态了么= =），然后发现它确实是有性质的（还是看代码吧= =），然后可以搞到线性的。
#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 1000050
#define M 1000000007
#define ll long long
ll ans;
int la[N],h[N],n,m,t;
char b[N];
int main()
{
int i,j,k,l,q,w,e;
memset(la,0,sizeof(la));memset(h,0,sizeof(h));
scanf("%d ",&t);
while (t--)
{
gets(b);n=strlen(b);h[1]=ans=1;
for (i=2;i<=n;i++)
{
k=la[i-1];
while (k&&b[k]!=b[i-1]) k=la[k];
if (b[k]==b[i-1]) la[i]=k+1;else la[i]=0;
h[i]=h[la[i]]+1;
}
k=0;
for (i=2;i<=n;i++)
{
while (k&&b[k]!=b[i-1]) k=la[k];
if (b[k]==b[i-1]) k++;
while (k>(i>>1)) k=la[k];
ans=(ans*(h[k]+1))%M;
}
printf("%lld\n",ans);
}
return 0;
}
BZOJ3671随机数生成器：感觉题目一大串其实还不就是暴力，但是各种时间空间卡常数卡的丧心病狂，一开始用函数递归打标记MLE，然后用queue也是挂，然后换成了数组，最后把快读的变量都考虑进去了，都过不了= =，后来知道了还是要对于每一行维护左右边界，虽然复杂度一样，但是比起我这种常数还是要小些。
#include <iostream>
#include <string.h>
#include <cmath>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
#define N 5050
#define ll long long
struct Point
{
int a1,a2;
};
ll a,b,c,d,x0;
int n,m,nm,wz[N*N],t[N*N],le[N],ri[N];
inline int Read()
{
int x=0;char y;
do y=getchar(); while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return x;
}
void Sign(int x,int y)
{
for (int i=1;i<=n;i++)
if (i<x) ri[i]=min(ri[i],y);else
if (i>x) le[i]=max(le[i],y);
return;
}
int main()
{
ll i,j,k,l,q,w,e;
cin >>x0>>a>>b>>c>>d>>n>>m>>nm;k=n*m;e=n+m-1;
for (i=1;i<=k;i++) t[i]=i;
for (i=1;i<=k;i++)
x0=((a*x0+b)*x0+c)%d,swap(t[x0%i+1],t[i]);
for (i=1;i<=nm;i++)
swap(t[q=Read()],t[l=Read()]);
for (i=1;i<=n;i++)
le[i]=1,ri[i]=m;
for (i=1;i<=k;i++)
wz[t[i]]=i;
for (i=1;i<=k;i++)
{
q=(wz[i]-1)%m+1;w=(wz[i]-1)/m+1;
if (q>=le[w]&&q<=ri[w])
{
if (--e)
printf("%d ",i);else
{printf("%d\n",i);break;}
Sign(w,q);
}
}
return 0;
}
BZOJ3240矩阵游戏：总记得之前分析过复杂度，总觉得是可以过的= =后来猜结论发现可以套费马小定理上去，然后就高精度都不用就水过了。
#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define M 1000000007
#define ll long long
#define ld long double
struct Point
{
ll a1,a2;
};
Point Read()
{
ll x=0,z=0;char y;
do y=getchar(); while (y<'0'||y>'9');
do x=(x*10+y-'0')%(M-1),z=(z*10+y-'0')%M,
y=getchar(); while (y>='0'&&y<='9');
return (Point){x,z};
}
inline ll Quick_Multi(ll x,ll y)
{
ll i=x*y-(ll)((ld)x/M*y+1e-9)*M;
return i<0?i+M:i;
}
inline Point Multi(Point x,Point y)
{
return (Point){Quick_Multi(x.a1,y.a1),
(Quick_Multi(x.a2,y.a1)+y.a2)%M};
}
Point Quick_Mi(Point x,ll y)
{
Point z;z.a1=1;z.a2=0;
while (y)
{
if (y&1) z=Multi(z,x);
x=Multi(x,x);
y >>= 1;
}
return z;
}
int main()
{
int i,j;Point k,l,q,w,e,n,m;
n=Read();m=Read();k.a1=(e=Read(),e.a1);k.a2=(e=Read(),e.a1);
l.a1=(e=Read(),e.a1);l.a2=(e=Read(),e.a1);
q=k.a1!=1?Quick_Mi(k,(m.a1+M-2)%(M-1)):
(Point){1,((m.a2-1)*k.a2)%M};
w=Multi(q,l);
w=w.a1!=1?Quick_Mi(w,(n.a1+M-2)%(M-1)):
(Point){1,((n.a2-1)*w.a2)%M};
w=Multi(w,q);
cout <<(w.a1+w.a2)%M<<endl;
return 0;
}
BZOJ2875随机数生成器：裸矩乘
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
#define ll long long
struct Point
{
ll a1,a2;
};
ll n,m,s;
inline ll Multi(ll x,ll y)
{
ll z=0;
while (y)
{
if (y&1) z=(z+x)%m;
x=(x+x)%m;
y >>= 1;
}
return z;
}
inline Point Mult(Point x,Point y)
{
return (Point){Multi(x.a1,y.a1),(Multi(x.a2,y.a1)+y.a2)%m};
}
inline Point Quick_mi(Point x,ll y)
{
Point z;z.a1=1;z.a2=0;
while (y)
{
if (y&1) z=Mult(z,x);
x=Mult(x,x);
y >>= 1;
}
return z;
}
int main()
{
int i,j;ll k,l;Point q,w,e;
cin >>m>>q.a1>>q.a2>>k>>n>>s;
q=Quick_mi(q,n);
k=((Multi(q.a1,k)+q.a2)%m)%s;
cout <<k<<endl;
}
BZOJ2878迷失游乐园：如果是树就是树形DP，否则环上情况特殊考虑，由于环很小甚至环上可以有k^2级别的处理。
#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 100050
#define ld long double
double h[N],s[N],ans,v[N];
int fi[N],c[N*2][3],ss=1,n,m,cl[N],d[N],le,ri,li[N];
bool b[N],f[N];
inline int Read()
{
int x=0;char y;
do y=getchar(); while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return x;
}
inline void Line(int x,int y,int z)
{
c[++ss][0]=y;c[ss][1]=fi[x];c[ss][2]=z;fi[x]=ss;
c[++ss][0]=x;c[ss][1]=fi[y];c[ss][2]=z;fi[y]=ss;
d[x]++;d[y]++;
return;
}
double DF1(int x,int y)
{
int l=0;
for (int i=fi[x];i;i=c[i][1])
if (c[i][0]!=y&&!b[c[i][0]])
h[x]+=c[i][2]+DF1(c[i][0],x),l++;
return l?(h[x]/=l):0;
}
void DS1(int x,int y,int z)
{
int i;double j=h[x];
h[x]=0;
for (i=fi[x];i;i=c[i][1])
if (c[i][0]!=y) h[x]+=h[c[i][0]]+c[i][2];
if (y)
h[x]+=z+(d[y]>1?(h[y]-j-z)/(d[y]-1):0);
ans+=h[x]/d[x];
for (i=fi[x];i;i=c[i][1])
if (c[i][0]!=y)
DS1(c[i][0],x,c[i][2]);
return;
}
void So1()
{
DF1(n,0);
DS1(n,0,0);
printf("%.8lf\n",ans/n);
return;
}
bool Find(int x,int y,int z)
{
b[li[y]=x]=1;
for (int i=fi[x];i;i=c[i][1])
if (b[c[i][0]]&&(i^1)!=z)
{
le=c[i][0];li[ri=y]=i;return 1;
}else
if (!b[c[i][0]]&&(li[y]=i,Find(c[i][0],y+1,i))) return 1;
return 0;
}
double DF2(int x)
{
int i,j,k,l=0;double q,w,e=0;
f[x]=1;
for (i=fi[x];i;i=c[i][1])
if (b[c[i][0]]&&!f[c[i][0]])
e+=c[i][2]+DF2(c[i][0]),l++;else
if (!b[c[i][0]])
e+=h[c[i][0]]+c[i][2],l++;
if (!l) l=1;
f[x]=0;v[x]=e;
return e/l;
}
void So2()
{
int i,j,k,l,q,w,e;
Find(1,1,0);
for (i=ri;i&&c[li[i-1]][0]!=le;i--);
if (!i) i++;
memset(b,0,sizeof(b));
for (j=i;j<=ri;j++) b[li[j-i+1]=c[li[j]][0]]=1;
for (j=1,ri=ri-i+1;j<=ri;j++)
DF1(li[j],0);
for (i=1;i<=ri;i++)
h[li[i]]=DF2(li[i]),ans+=h[li[i]],h[li[i]]=v[li[i]];
for (i=1;i<=ri;i++)
for (j=fi[li[i]];j;j=c[j][1])
if (!b[c[j][0]])
DS1(c[j][0],li[i],c[j][2]);
printf("%.8lf\n",ans/n);
return;
}
int main()
{
int i,j,k,l,q,w,e;
scanf("%d%d",&n,&m);ans=0;
for (i=1;i<=m;i++)
q=Read(),w=Read(),e=Read(),Line(q,w,e);
if (m<n)
So1();else
So2();
return 0;
}
BZOJ2877魔幻棋盘：
没看出来，感觉二维差分是很神啊，具体题解移步这里，然后就是写一个二维线段树了= =
然而中间有一个地方写挂了一直没调出来wa了几次真是羞耻= =不过感觉还是很容易写挂啊
而且40+个if真是sxbk。也不知道网上有的人写400+是怎么做到的（以前我好像写裸的splay也写过400+现在感觉真是厉害）
#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
#define N 500050
#define ll long long
ll t,n,m,X,Y,st=0,ss=0,d[N*5],s=0,INF=100000000151234567;
struct Seg_Tree
{
ll v;Seg_Tree* c[2];
} b[N*10];
struct Ment_Tree
{
Seg_Tree* t;Ment_Tree* c[2];
} a[N*4];
inline ll Read()
{
ll x=0;char y;bool z=0;
do y=getchar(),z|=y=='-'; while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return z?-x:x;
}
inline ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);}
inline ll Num(int x,int y)
{return d[(x-1)*m+y];}
inline ll Abs(ll x)
{return x<0?-x:x;}
inline ll Calc(int x,int y)
{
if (x<X&&y<Y) return Num(x,y)-Num(x+1,y)-Num(x,y+1)+Num(x+1,y+1);
if (x>X&&y<Y) return Num(x,y)-Num(x-1,y)-Num(x,y+1)+Num(x-1,y+1);
if (x<X&&y>Y) return Num(x,y)-Num(x+1,y)-Num(x,y-1)+Num(x+1,y-1);
if (x>X&&y>Y) return Num(x,y)-Num(x-1,y)-Num(x,y-1)+Num(x-1,y-1);
if (x==X&&y==Y) return Num(x,y);
if (x==X&&y<Y) return Num(x,y)-Num(x,y+1);
if (x==X&&y>Y) return Num(x,y)-Num(x,y-1);
if (x<X&&y==Y) return Num(x,y)-Num(x+1,y);
return Num(x,y)-Num(x-1,y);
}
Seg_Tree* DSF(int x,int y,int z)
{
int i=(x+y)/2,j=++st;
if (x==y) b[j].v=Calc(z,x),b[j].c[0]=b[j].c[1]=NULL;else
b[j].c[0]=DSF(x,i,z),b[j].c[1]=DSF(i+1,y,z),
b[j].v=gcd(b[j].c[0]->v,b[j].c[1]->v);
return &b[j];
}
Seg_Tree* Merge(int x,int y,Seg_Tree* z,Seg_Tree* o)
{
int i=(x+y)/2,j=++st;
b[j].v=gcd(z->v,o->v);
if (x==y) b[j].c[0]=b[j].c[1]=NULL;else
b[j].c[0]=Merge(x,i,z->c[0],o->c[0]),
b[j].c[1]=Merge(i+1,y,z->c[1],o->c[1]);
return &b[j];
}
Ment_Tree* DFS(int x,int y)
{
int i=(x+y)/2,j=++ss;
if (x==y)
a[j].t=DSF(1,m,x);else
a[j].c[0]=DFS(x,i),a[j].c[1]=DFS(i+1,y),
a[j].t=Merge(1,m,a[j].c[1]->t,a[j].c[0]->t);
return &a[j];
}
ll QueSeg(int x,int y,Seg_Tree* z,int o,int p)
{
int i=(x+y)/2;ll j=-INF,k=-INF;
if (x==o&&y==p) return z->v;
if (o<=i) j=QueSeg(x,i,z->c[0],o,min(p,i));
if (p>i) k=QueSeg(i+1,y,z->c[1],max(o,i+1),p);
if (j==-INF) return k;else
return k==-INF?j:Abs(gcd(k,j));
}
ll QueMent(int x,int y,Ment_Tree* z,int o,int p,int u,int v)
{
int i=(x+y)/2;ll j=-INF,k=-INF;
if (x==o&&y==p) return QueSeg(1,m,z->t,u,v);
if (o<=i) j=QueMent(x,i,z->c[0],o,min(p,i),u,v);
if (p>i) k=QueMent(i+1,y,z->c[1],max(o,i+1),p,u,v);
if (j==-INF) return k;else
return k==-INF?j:Abs(gcd(k,j));
}
void ModiSeg(int x,int y,Seg_Tree* z,int o,ll p)
{
int i=(x+y)/2;
if (x==y) {z->v+=p;return;}
if (o<=i) ModiSeg(x,i,z->c[0],o,p);else
ModiSeg(i+1,y,z->c[1],o,p);
z->v=gcd(z->c[0]->v,z->c[1]->v);
return;
}
void Modify(int x,int y,Seg_Tree* z,Seg_Tree* o,Seg_Tree* p,ll u)
{
int i=(x+y)/2;
z->v=gcd(o->v,p->v);
if (x==y) return;
if (u<=i) Modify(x,i,z->c[0],o->c[0],p->c[0],u);else
Modify(i+1,y,z->c[1],o->c[1],p->c[1],u);
return;
}
void ModiMent(int x,int y,Ment_Tree* z,int o,int p,ll u)
{
int i=(x+y)/2;
if (x==y) {ModiSeg(1,m,z->t,p,u);return;}
if (o<=i) ModiMent(x,i,z->c[0],o,p,u);else
ModiMent(i+1,y,z->c[1],o,p,u);
Modify(1,m,z->t,z->c[0]->t,z->c[1]->t,p);
return;
}
void Revise()
{
ll i,j,k=Read(),q=Read(),l=Read(),w=Read(),e=Read();
if (k<=X&&l>=X&&q<=Y&&w>=Y) ModiMent(1,n,&a[1],X,Y,e);
if (k<=X&&l>=X&&q<=Y&&q-1) ModiMent(1,n,&a[1],X,q-1,-e);
if (k<=X&&l>=X&&w>=Y&&w!=m) ModiMent(1,n,&a[1],X,w+1,-e);
if (k<=X&&l>=X&&q>Y) ModiMent(1,n,&a[1],X,q,e);
if (k<=X&&l>=X&&w<Y) ModiMent(1,n,&a[1],X,w,e);
if (q<=Y&&w>=Y&&k<=X&&k-1) ModiMent(1,n,&a[1],k-1,Y,-e);
if (q<=Y&&w>=Y&&l>=X&&l!=n) ModiMent(1,n,&a[1],l+1,Y,-e);
if (q<=Y&&w>=Y&&k>X) ModiMent(1,n,&a[1],k,Y,e);
if (q<=Y&&w>=Y&&l<X) ModiMent(1,n,&a[1],l,Y,e);
if (k<=X&&q<=Y&&k-1&&q-1) ModiMent(1,n,&a[1],k-1,q-1,e);
if (k<=X&&q>Y&&k-1) ModiMent(1,n,&a[1],k-1,q,-e);
if (k>X&&q<=Y&&q-1) ModiMent(1,n,&a[1],k,q-1,-e);
if (k>X&&q>Y) ModiMent(1,n,&a[1],k,q,e);
if (k<=X&&w>=Y&&k-1&&w!=m) ModiMent(1,n,&a[1],k-1,w+1,e);
if (k<=X&&w<Y&&k-1) ModiMent(1,n,&a[1],k-1,w,-e);
if (k>X&&w>=Y&&w!=m) ModiMent(1,n,&a[1],k,w+1,-e);
if (k>X&&w<Y) ModiMent(1,n,&a[1],k,w,e);
if (l>=X&&q<=Y&&l!=n&&q-1) ModiMent(1,n,&a[1],l+1,q-1,e);
if (l>=X&&q>Y&&l!=n) ModiMent(1,n,&a[1],l+1,q,-e);
if (l<X&&q<=Y&&q-1) ModiMent(1,n,&a[1],l,q-1,-e);
if (l<X&&q>Y) ModiMent(1,n,&a[1],l,q,e);
if (l>=X&&w>=Y&&l!=n&&w!=m) ModiMent(1,n,&a[1],l+1,w+1,e);
if (l>=X&&w<Y&&l!=n) ModiMent(1,n,&a[1],l+1,w,-e);
if (l<X&&w>=Y&&w!=m) ModiMent(1,n,&a[1],l,w+1,-e);
if (l<X&&w<Y) ModiMent(1,n,&a[1],l,w,e);
return;
}
int main()
{
ll i,j,k,l,q,w,e;
n=Read();m=Read();X=Read();Y=Read();t=Read();
for (i=1;i<=n*m;i++) d[i]=Read();
DFS(1,n);
for (i=1;i<=t;i++)
if (!Read())
{
k=Read(),l=Read(),q=Read(),w=Read(),s++,
printf("%lld\n",QueMent(1,n,&a[1],X-k,X+q,Y-l,Y+w));
}else
Revise();
return 0;
}
BZOJ2435道路修建：
做法一眼，但是之前一直不知道递归层数5w+就会爆炸的【捂脸贼】，所以搞成DFS序再搞
#include <iostream>
#include <cmath>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
#define N 1000050
#define ll long long
ll ans=0;
int c[N*2][3],b[N],fa[N],fi[N],s[N],a[N],n,m,ss=1;
inline int Read()
{
int x=0;char y;
do y=getchar(); while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return x;
}
inline void Line(int x,int y,int z)
{
c[++ss][0]=y;c[ss][1]=fi[x];c[ss][2]=z;fi[x]=ss;
c[++ss][0]=x;c[ss][1]=fi[y];c[ss][2]=z;fi[y]=ss;
return;
}
void BFS()
{
int i,j,k,l,q,w,e,ri=1;
b[1]=1;fa[1]=-1;
for (i=1;i<=n;i++)
{
for (j=fi[b[i]];j;j=c[j][1])
if (!fa[c[j][0]])
fa[c[j][0]]=b[i],b[++ri]=c[j][0],
a[c[j][0]]=c[j][2];
s[i]=1;
}
for (i=n;i>=1;i--)
for (j=fi[b[i]];j;j=c[j][1])
if (c[j][0]!=fa[b[i]])
s[b[i]]+=s[c[j][0]];
for (i=2;i<=n;i++)
ans+=(ll)(a[i])*abs(n-s[i]*2);
return;
}
int main()
{
int i,j,k,l,q,w,e;
n=Read();
for (i=1;i<n;i++)
q=Read(),w=Read(),e=Read(),Line(q,w,e);
BFS();
cout <<ans<<endl;
return 0;
}
BZOJ2434阿狸的打字机：
首先AC自动机是肯定的，但是爆力kmp会挂。所以考虑优化，首先询问可以变成y串上面有多少个i使得yi可以通过fail指针转移到x串的末尾，所以考虑建fail树，然后维护关于DFS序的线段树，初始权值全部为0，在AC自动机上DFS，每经过一个点就使其权值加1，遇到询问就查询x串末尾所对应的子树和，离开时也要权值-1。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <queue>
using namespace std;
#define N 100050
#define ll long long
int n,m,ss=0,qu[N][3],fi[N],li[N],s=0,sg[N][2];char d[N];
int fr[N],nr[N];
queue <int> list;
struct Trie
{
int fa[N],ne[N],fi[N],v[N];
} a;
struct Fail
{
int fa[N],ne[N],fi[N];
} b;
struct Segment_Tree
{
int c[N*3][2],s[N];
} c;
inline int Read()
{
int x=0;char y;
do y=getchar(); while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return x;
}
/*
void DFF(int x)
{
cout <<x<<' '<<b.fa[x]<<' '<<b.ne[x]<<' '<<b.fi[x]<<endl;
if (b.fi[x]) DFF(b.fi[x]);
if (b.ne[x]) DFF(b.ne[x]);
return;
}*/
inline void Get(int x,int y)
{
b.fa[x]=y;b.ne[x]=b.fi[y];b.fi[y]=x;return;
}
void Set_Up()
{
int i,j,k,l,q,w,e;
list.push(0);
while (!list.empty())
{
k=list.front();list.pop();
for (i=a.fi[k];i;i=a.ne[i])
{
list.push(i);q=b.fa[k];
while (q)
{
for (j=a.fi[q];j;j=a.ne[j])
if (a.v[j]==a.v[i])
{Get(i,j);break;}
if (b.fa[i]) break;
q=b.fa[q];
}
if (!q&&!b.fa[i])
{
for (j=a.fi[0];j;j=a.ne[j])
if (a.v[j]==a.v[i]&&i!=j)
{Get(i,j);break;}
if (!b.fa[i]) Get(i,0);
}
}
}
return;
}
void Set_up()
{
int i,j,k,l,q,w,e=0;
for (i=0;i<n;i++)
if (d[i]=='B') e=a.fa[e];else
if (d[i]=='P')
li[++s]=e,nr[s]=fr[e],fr[e]=s;else
{
k=0;
for (j=a.fi[e];j;j=a.ne[j])
if (a.v[j]==d[i])
{k=e=j;break;}
if (k==0)
{
a.v[++ss]=d[i];a.fa[ss]=e;
a.ne[ss]=a.fi[e];a.fi[e]=ss;e=ss;
}
}
ss=0;
Set_Up();
return;
}
void Sign(int x)
{
sg[x][0]=++ss;
for (int i=b.fi[x];i;i=b.ne[i])
Sign(i);
sg[x][1]=ss;
return;
}
void Insert(int x,int y,int z,int o,int p)
{
int i=(x+y)/2,j=z*2;
c.s[z]+=p;
if (x==y) return;
if (o>i)
Insert(i+1,y,j+1,o,p);else
Insert(x,i,j,o,p);
return;
}
int Query(int x,int y,int z,int o,int p)
{
int i=(x+y)/2,j=z*2,k=0;
if (x==o&&y==p) return c.s[z];
if (o<=i) k=Query(x,i,j,o,min(i,p));
if (p>i) k+=Query(i+1,y,j+1,max(o,i+1),p);
return k;
}
void DFS(int x)
{
Insert(1,ss,1,sg[x][0],1);
for (int i=fr[x];i;i=nr[i])
for (int j=fi[i];j;j=qu[j][1])
qu[j][2]=Query(1,ss,1,sg[li[qu[j][0]]][0],sg[li[qu[j][0]]][1]);
for (int i=a.fi[x];i;i=a.ne[i])
DFS(i);
Insert(1,ss,1,sg[x][0],-1);
return;
}
int main()
{
scanf("%s",d);n=strlen(d);
Set_up();Sign(0);m=Read();
for (int i=1,k;i<=m;i++)
qu[i][0]=Read(),qu[i][1]=fi[k=Read()],fi[k]=i;
DFS(0);
for (int i=1;i<=m;i++)
printf("%d\n",qu[i][2]);
return 0;
}
BZOJ2007海拔：
可以自行YY到一个性质：这些数要不就是0要不就是1（话说题目下面那个提示：海拔也有可能是小数也是sxbk），因为最优方案中最大的数如果调整到旁边的数的大小是可以使答案更优的，最小的也是这样。所以最优方案中最大的数一定是1、最小的一定是0，同理通过调整不存在小数，而且不存在不包含左上角的0连通块和不包含右下角的1连通块，因为这些连通块全部取反之后是会更优的。所以最后就变成了求一个最小割了，由于是平面图，而且点数艹蛋，所以转成对偶图用最短路问题做。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <queue>
using namespace std;
#define N 550
#define M 1500000
#define INF 0x7f7f7f7f
int h[M],fi[M],c[M][3],n,m,S=M-1,T=M-2,sg[N][N],ss=1,st=0;
int a[N][N][4];
bool b[M];
queue <int> li;
inline int Read()
{
int x=0;char y;
do y=getchar(); while (y<'0'||y>'9');
do x=x*10+y-'0',y=getchar(); while (y>='0'&&y<='9');
return x;
}
inline void Line(int x,int y,int z,int o)
{
c[++ss][0]=y;c[ss][1]=fi[x];c[ss][2]=z;fi[x]=ss;
c[++ss][0]=x;c[ss][1]=fi[y];c[ss][2]=o;fi[y]=ss;
return;
}
void Set_up()
{
int i,j,k,l,q,w,e;
for (i=1;i<=n;i++)
sg[0][i]=sg[i][n+1]=S,sg[n+1][i]=sg[i][0]=T;
for (i=1;i<=n;i++)
for (j=1;j<=n;j++) sg[i][j]=++st;
for (i=0;i<=n;i++)
for (j=1;j<=n;j++)
a[i][j][3]=Read();
for (i=1;i<=n;i++)
for (j=0;j<=n;j++)
a[i][j+1][4]=Read();
for (i=0;i<=n;i++)
for (j=1;j<=n;j++)
a[i+1][j][1]=Read();
for (i=1;i<=n;i++)
for (j=0;j<=n;j++)
a[i][j][2]=Read();
for (int i=1;i<=n;i++)
for (int j=0;j<=n;j++)
Line(sg[i][j],sg[i][j+1],a[i][j][2],a[i][j+1][4]);
for (int i=0;i<=n;i++)
for (int j=1;j<=n;j++)
Line(sg[i][j],sg[i+1][j],a[i][j][3],a[i+1][j][1]);
return;
}
void SPFA()
{
int i,j,k,l,q,w,e;
li.push(S);b[S]=1;h[T]=INF;h[S]=0;
for (i=1;i<=st;i++) h[i]=INF;
while (!li.empty())
{
q=li.front();li.pop();b[q]=0;
for (i=fi[q];i;i=c[i][1])
if (h[q]+c[i][2]<h[c[i][0]])
{
h[c[i][0]]=h[q]+c[i][2];
if (!b[c[i][0]])
li.push(c[i][0]),b[c[i][0]]=1;
}
}
return;
}
int main()
{
int i,j,k,l,q,w,e;
n=Read();Set_up();
SPFA();
printf("%d\n",h[T]);
return 0;
}
BZOJ2005能量采集
本来打算放到“数学相关”里面，但是太影响排版了，而且这种神题还是单独放比较好。
一共有四种做法：
首先题目可以化成一个2*ΣΣgcd(i,j)-nm是显然的，至于前面的求法听说有好几种做法
做法一：From KZF：
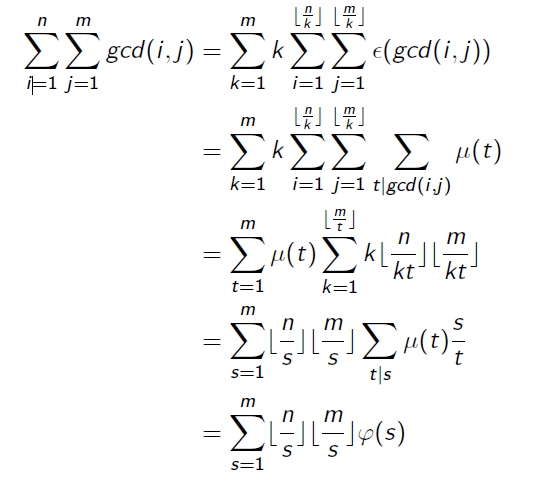
首先线性筛出欧拉函数，然后直接求解，时间也是线性的。
做法二：From 小狗：
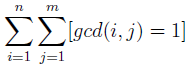对于左式可以将其化成
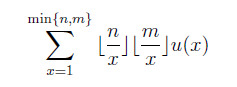
然后[n/x][m/x]可以分成O(sqrt(n)+sqrt(m))段，可以预处理u(x)前缀和在根号时间内求解
所以代入kzf的第一行的式子中O(nsqrt(n))级别的。
做法三：From wulala：
要求每个数是多少个数对的gcd，可以用类似容斥但更SB的方法：首先最多这个数可以作为(n/i)*(m/i)个数对的公因数，然后减去所有gcd是i的倍数的数对，所以时间复杂度就是Σn/i，也就是调和级数，O(n log n)
做法四：From KZF：
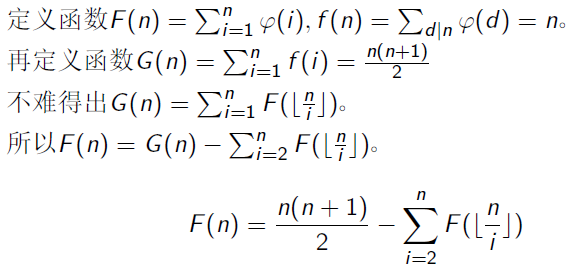
可以先预处理出n^(2/3)的F(n)，然后将KZF最后面的那个式子分成根号块，每块求值据说是O(n^(1/6))，然后复杂度就喜闻乐见O(n^(2/3))
神奇的是，上面四种做法复杂度都不一样= =，但是水B的数据范围应该是都能让过的。
最近几次考试题
从最近几次的考试题里面放几道上来好了
最近的NOIP赛的题目比较水，但是我为毛总是不想写对拍= =，所以一直没拉开分差，也没有AK过。
唯一在考场上面没想出来的是一道搜索题：就是要搞一个多维背包。考试的时候就觉得不可做，于是觉得应该是要搜索，但是总感觉维数大小是50会挂，而且这种题目让人感觉贪心可以骗些分的样子，我这种逗了一B的代码能力也就随便写了个贪心。最后题解里面说是要加一堆的优化：主要是物品的大小有很多重复的，这些就需要决策单调性，而且还有个边界判断后面还有没有解。虽然感觉还是很不科学，但是确实是能过的= =
补：10号也考了一场。duyege差点AK但是第三题我并没有想出来，想想当时的状态虽然一直在想但是很快就走神了，而且当时我也不知为何没有那么强的做出这道题的欲望。（我为毛这么萎啊！）后来看式子的时候也是感觉得了智商癌，一直没看懂。
题意：给定数组B，第i位代表A数组前i位有多少个小于等于i的数，求有多少个满足条件的A数组，并且A数组是一个1-n的排列。
题解：“很简单啊！”。当b[i]-b[i-1]=1时说明要不就是第i位有一个1-i之间的数，要不就是第1-i-1位有一个i，所以答案乘以2*(i-1-b[i-1])+1；当b[i]-b[i-1]=2时说明第i位有一个1-i-1之间的数，并且第1-i-1位有一个i，所以答案乘以(i-1-b[i-1])^2。回想我的思路我一直觉得如果设前i位有多少种方案是会有问题的，于是一直没往这方面想，现在想想真是SB。
还有一些NOI的模拟赛，有的题目如果放到NOIP的模拟赛中我是可以想出来的，但是我总是觉得这些题会很神，所以就没认真去想。而且这两天的状态是真心萎废，甚至考试中可以做到一道题调一个上午。感觉还是心态问题，考的人里面还有某爷、某司机什么的，总觉得自己完全不可能在这些人中间考好，完全没有进入考试状态，而且总是很容易就弃疗了。但是实力不会等于成绩啊，我有几次还是有考好的机会的，而且我完全不能是因为为了考好而考试，有的题目做起来本身就应该是愉快的啊。
不多说了还是放题目吧：就是有一个数列的第一项v0给出来了，然后有s1项每一项是前一项+1，还有s2项每一项是前一位的2倍，然后后面就是ai=ai-1*……ai-k，k<=101,N<=1e9，要求数列第N项对1e8+7取模。
题解：这东西肯定没办法直接搞，所以要想办法让递推式能用矩阵乘法优化。所以想到用让ai取log然后就可以用矩阵乘法搞了，但是由于取过了log所以没办法取模，肯定会有太大了，而且还会有精度问题，算它的幂，所以要想办法尽量不用log。而且矩阵乘法的递推矩阵是没有实数的，所以我们没必要取log，只要将递推矩阵快速幂之后的最后一次矩阵乘法化乘法为幂运算就可以了，由于最后一次是幂运算，而且用于取模的数是素数，所以在矩阵快速幂的时候就可以用费马小定理模P-1。感觉就是一堆东西杂在一起，并不算难。然后被细节坑到了30分，体会到了不写对拍的快感。
#include <iostream>
#include <cmath>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
#define N 205
#define M 100000007
#define eps 1e-9
#define ll long long
struct Matrix
{
ll a[N][N];
} emp,E,ans;
ll v0,s1,s2,m,n,t;
inline ll Quick_mi(ll x,ll y)
{
ll z=1;
while (y)
{
if (y&1) z=(z*x)%M;
x=(x*x)%M;
y/=2;
}
return z;
}
inline Matrix* Multi(Matrix *x,Matrix *y)
{
Matrix *z=(Matrix*)(malloc(sizeof(Matrix)));
*z=emp;
for (int i=1;i<=m;i++)
for (int j=1;j<=m;j++)
for (int k=1;k<=m;k++)
z->a[i][k]+=x->a[i][j]*y->a[j][k];
for (int i=1;i<=m;i++)
for (int j=1;j<=m;j++)
z->a[i][j]%=M-1;
return z;
}
inline Matrix* Quick_mi(Matrix *x,ll y)
{
Matrix *z;
z=(Matrix*)(malloc(sizeof(Matrix)));
*z=E;
while (y)
{
if (y&1) z=Multi(z,x);
x=Multi(x,x);
y/=2;
}
return z;
}
int main()
{
int i,j;Matrix q,w,*e;ll k,l;double o,p;
scanf("%d",&t);
while (t--)
{
memset(emp.a,0,sizeof(emp.a));memset(E.a,0,sizeof(E.a));
memset(q.a,0,sizeof(q.a));memset(ans.a,0,sizeof(ans.a));
memset(w.a,0,sizeof(w.a));
scanf("%d%d%d%d%d",&v0,&s1,&s2,&m,&n);
for (i=1;i<=m;i++)
E.a[i][i]=1;
for (i=1;i<=m;i++)
w.a[i][i-1]=w.a[i][m]=1;
for (i=1;i<=m;i++)
for (j=1;j<=m;j++)
ans.a[i][j]=1;
if (n<=s1+1)
{cout <<v0+(n-1)<<endl;continue;}
k=v0+s1;
if (n<=s2+s1+1)
{cout <<(k*Quick_mi(2,n-s1-1))%M<<endl;continue;}
if (m==s2+s1+1)
{
q.a[1][1]=v0;
for (i=s1+1;i>=2;i--)
q.a[1][i]=k--;
k+=s1;
for (i=m-s2+1;i<=m;i++)
q.a[1][i]=(k=(k*2)%M);
}else
if (m<=s2)
{
k=(k*Quick_mi(2,s2-m))%M;
for (i=1;i<=m;i++)
k=(k*2)%M,q.a[1][i]=k;
}else
{
for (i=m-s2;i>=1;i--)
q.a[1][i]=k--;
k+=m-s2;
for (i=m-s2+1;i<=m;i++)
q.a[1][i]=(k=(k << 1)%M);
}
e=Quick_mi(&w,n-s2-s1-1);
for (i=1;i<=m;i++)
for (j=1;j<=m;j++)
ans.a[1][j]=(ans.a[1][j]*Quick_mi(q.a[1][i],e->a[i][j]))%M;
printf("%d\n",(int)(ans.a[1][m]%M));
}
return 0;
}
有道题由于第一题看错题一直觉得是FFT于是试着在考场上搞出FFT，所以没怎么想第三题，后来发现确实不难= =。
题意：有一个字符串，一开始只有大写字母，然后可以往中间加下划线、交换任意两个字符或者删字符。要求最终串的长度为N，任意两个相同的字母之间有至少k个比它大的字符（设下划线的ASCII码最大）。
题解：可以字母从小到大搞，设a[i][j]为搞到第i个字符还有j个空位的方案数，对于那个两个相同字母之间的限制可以直接组合数搞。但是N最大可能有1Y，原串最大2K+，所以只要把j换成用了j个位置，然后就可以直接DP了。（然而我还并没有写= =）
还有道题：要将1-n分成两个集合，使得不存在不同的三个数x、y、z同时存在一个集合里面使得xy=z。n<=10w
题解：考场上面就觉得很神，于是照着它给的50分线也就是n<=50交了张表，就没想太多了= =。后来题解里面说n>96时答案就是0了，于是应该交一张96的表就可以A了= =。出题人sxbk！
最近做了两套汪文潇和镇海的卷子，都考爆了，两天不仅成绩不好，而且还被自己wgy和Fadeness虐了（虽然两个都是因为数据水A的题），跟前几次集训状态相比感觉在考场上面能想出正解了（然并卵），然而还是会考挂，一是思路不清晰，很容易想错或者看错题，所以只写对了暴力完全就没有任何优势，二虽然这两场不明显，但是感觉还是代码能力弱了。除了能力问题就是整个人真的状态很萎，还是很容易弃疗，对自己还是太不自信了，有的时候真的觉得自己太弱了。还有就是最近实在是太摆了，说好的刷题量完全没上去。话说我这么萎我还能撑到什么时候？
题意：有两个长度为n的序列a、b，序列里面的每个数在1~n之间，求有多少个长度为n的排列c，使得a[c[i]]=c[b[i]]，并输出其中一个方案
题解：第一次感觉自己的思维还不是那么没救，虽然在考试最后30分钟想出来也没什么用= =。想了个把小时= =，首先看到问题感觉是置换群相关，或许会是polya计数法的奇怪运用？一直在画映射的图，感觉记不起来有什么相似的模型，想了很久差点就要弃(shui)疗(zhao)了，然后脑洞了一下试了下将这个画成第二题的环套树森林，就是对于每个i，i的父亲是a[i]，然后成了一个环套树，b也这么建，然后看图就可以很容易知道题目的要求变成了求a和b的映射使得两个森林同构。然后就可以有很多乱搞了。首先判断两个森林是不是同构的，这个总感觉最近碰到过一个相似的题目，但是那个是好像是用DP的= =，然而我感觉只会用hash的搞法。然后计算方案肯定是第i层的映射第i层的，尝试从第一层搞到最后一层，那么子树同构的结点肯定可以相互映射，那么如果a中有i个节点的子树同构，就可以把答案乘以i!，像这样子全部乘起来就是了= =那么环套树感觉又特殊一点，判断的时候用最小表示法，算的时候也是求出最小循环子串，貌似kmp相关？然后其他地方都差不多了吧，貌似求一组方案可以随便搞的样子。。。
题意：给定大小为20W的环套树森林，然后有20W组总共100W的染色，每组染色独立，染色是将一些点染成白点一些染成黑点，求每一组中“对于所有黑点是白点的祖先的二元组中黑点到白点路径上的边编号最大值”的最小值。
题解：题目是水题，但是艹蛋的题目大意（其实就是我语文不好啊！）坑了我两次，第一次naive我不记得是怎么理解的了，我竟然还写完了直到被样例卡住才反应过来，然后第二次我以为是求所有二元组中白点的父亲编号的最小值，然后一直在想线性做法= =（之前碰到过明明复杂度是n log n，而且n是100w的然后被卡掉了= =，这种情况后面也碰到过几次，完全搞怕了），最后还是写了线段树，如果理解对题意的话就应该还要加一个主席树查询最大值。如果根部有环的话就是缩点然后乱搞就是了（貌似这样还要加一棵主席树= =）总而言之如果没理解错题意感觉不难。
